Bubble Sort is a simple algorithm which is used to sort a given set of

Big O notation is used in Computer Science to describe the performance or complexity of an algorithm. Big O specifically describes the worst-case scenario, and can be used to describe the execution time required or the space used (e.g. in memory or on disk) by an algorithm. Anyone who's read Programming Pearls or any other Computer Science books and doesn’t have a grounding in Mathematics will have hit a wall when they reached chapters that mention O(N log N) or other seemingly crazy syntax. Hopefully this article will help you gain an understanding of the basics of Big O and Logarithms.
As a programmer first and a mathematician second (or maybe third or fourth) I found the best way to understand Big O thoroughly was to produce some examples in code. So, below are some common orders of growth along with descriptions and examples where possible.
Binary search is a technique used to search sorted data sets. It works by selecting the middle element of the data set, essentially the median, and compares it against a target value. If the values match it will return success. If the target value is higher than the value of the probe element it will take the upper half of the data set and perform the same operation against it. Likewise, if the target value is lower than the value of the probe element it will perform the operation against the lower half. It will continue to halve the data set with each iteration until the value has been found or until it can no longer split the data set.
This type of algorithm is described as O(log N). The iterative halving of data sets described in the binary search example produces a growth curve that peaks at the beginning and slowly flattens out as the size of the data sets increase e.g. an input data set containing 10 items takes one second to complete, a data set containing 100 items takes two seconds, and a data set containing 1000 items will take three seconds. Doubling the size of the input data set has little effect on its growth as after a single iteration of the algorithm the data set will be halved and therefore on a par with an input data set half the size. This makes algorithms like binary search extremely efficient when dealing with large data sets.
n elements provided in form of an array with n number of elements. Implementing Bubble Sort Algorithm
Following are the steps involved in bubble sort(for sorting a given array in ascending order):
- Starting with the first element(index = 0), compare the current element with the next element of the array.
- If the current element is greater than the next element of the array, swap them.
- If the current element is less than the next element, move to the next element. Repeat Step 1.
- In step 3, if If we have total
nelements, then we need to repeat this process forn-1times. - If we did 1st iteration last index is found and fixed, 2nd iternation n-2 times, 3rd iteration n-3 times.
- Hence formula is (n-1) + (n-2) + (n-3) + ..... + 3 + 2 + 1
Let's consider an array with values
{5, 1, 6, 2, 4, 3}
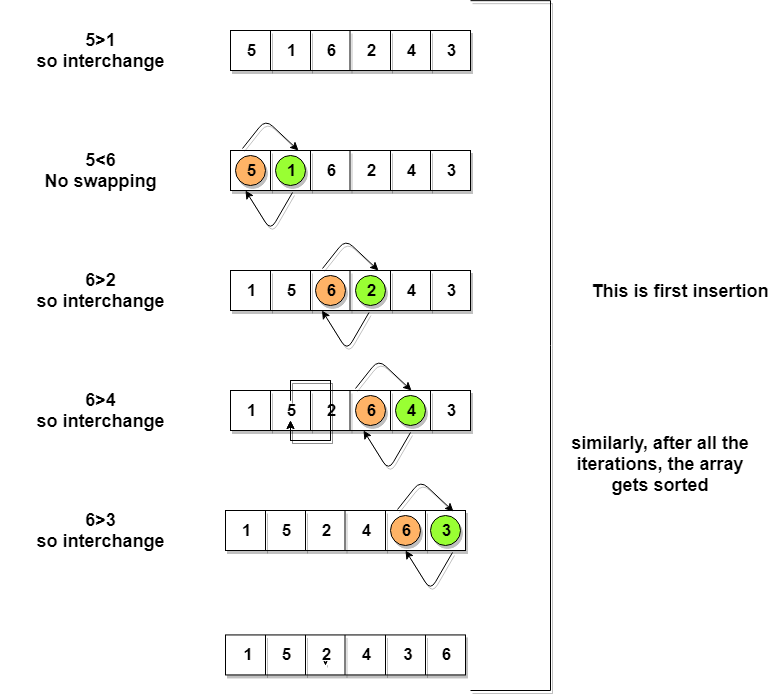
Below, we have a pictorial representation of how bubble sort will sort the given array.

So as we can see in the representation above, after the first iteration,
6 is placed at the last index, which is the correct position for it.
Similarly after the second iteration,
5 will be at the second last index, and so on.
Time to write the code for bubble sort:
/ below we have a simple C program for bubble sort
#include <stdio.h>
void bubbleSort(int arr[], int n)
{
int i, j, temp;
for(i = 0; i < n; i++)
{
for(j = 0; j < n-i-1; j++)
{
if( arr[j] > arr[j+1])
{
// swap the elements
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
// print the sorted array
printf("Sorted Array: ");
for(i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
}
int main()
{
int arr[100], i, n, step, temp;
// ask user for number of elements to be sorted
printf("Enter the number of elements to be sorted: ");
scanf("%d", &n);
// input elements if the array
for(i = 0; i < n; i++)
{
printf("Enter element no. %d: ", i+1);
scanf("%d", &arr[i]);
}
// call the function bubbleSort
bubbleSort(arr, n);
return 0;
}
Above algorithm is not efficient because as per the above logic, the outer
for loop will keep on executing for 6 iterations even if the array gets sorted after the second iteration.
So, we can clearly optimize our algorithm.
Optimized Bubble Sort Algorithm
To optimize our bubble sort algorithm, we can introduce a
flag to monitor whether elements are getting swapped inside the inner for loop.
If for a particular iteration, no swapping took place, it means the array has been sorted and we can jump out of the
for loop, instead of executing all the iterations.
Let's consider an array with values
{11, 17, 18, 26, 23}
Below, we have a pictorial representation of how the optimized bubble sort will sort the given array.

As we can see, in the first iteration, swapping took place, hence we updated our
flag value to 1, as a result, the execution enters the for loop again.
But in the second iteration, no swapping will occur,
hence the value of
flag will remain 0, and execution will break out of loop.// below we have a simple C program for bubble sort
#include <stdio.h>
void bubbleSort(int arr[], int n)
{
int i, j, temp;
for(i = 0; i < n; i++)
{
for(j = 0; j < n-i-1; j++)
{
// introducing a flag to monitor swapping
int flag = 0;
if( arr[j] > arr[j+1])
{
// swap the elements
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
// if swapping happens update flag to 1
flag = 1;
}
}
// if value of flag is zero after all the iterations of inner loop
// then break out
if(!flag)
{
break;
}
}
// print the sorted array
printf("Sorted Array: ");
for(i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
}
int main()
{
int arr[100], i, n, step, temp;
// ask user for number of elements to be sorted
printf("Enter the number of elements to be sorted: ");
scanf("%d", &n);
// input elements if the array
for(i = 0; i < n; i++)
{
printf("Enter element no. %d: ", i+1);
scanf("%d", &arr[i]);
}
// call the function bubbleSort
bubbleSort(arr, n);
return 0;
}
In the above code, in the function
bubbleSort, if for a single complete cycle of j iteration(inner forloop), no swapping takes place, then flag will remain 0 and then we will break out of the for loops, because the array has already been sorted.Complexity Analysis of Bubble Sort
In Bubble Sort,
n-1 comparisons will be done in the 1st pass, n-2 in 2nd pass, n-3 in 3rd pass and so on. So the total number of comparisons will be,
(n-1) + (n-2) + (n-3) + ..... + 3 + 2 + 1
Sum = n(n-1)/2
i.e O(n2)
Hence the time complexity of Bubble Sort is O(n2).
The main advantage of Bubble Sort is the simplicity of the algorithm.
The space complexity for Bubble Sort is O(1), because only a single additional memory space is required i.e. for
temp variable.
Also, the best case time complexity will be O(n), it is when the list is already sorted.
Following are the Time and Space complexity for the Bubble Sort algorithm.
- Worst Case Time Complexity [ Big-O ]: O(n2)
- Best Case Time Complexity [Big-omega]: O(n)
- Average Time Complexity [Big-theta]: O(n2)
- Space Complexity: O(1)
Others comment on Big 0, need to analyse, don't blindly take:
When calculating the Big-O complexity of an algorithm, the thing being shown is the factor that gives the largest contribution to the increase in execution time if the number of elements that you run the algorithm over increases.
If you have an algorithm with a complexity of
As the
(n^2 + n)/2 and you double the number of elements, then the constant 2 does not affect the increase in the execution time, the term n causes a doubling in the execution time and the term n^2 causes a four-fold increase in execution time.As the
n^2 term has the largest contribution, the Big-O complexity is O(n^2).2nd person(ShadSterling) thought:
It's not that "(n² + n)/2 behaves like n² when n is large", it's that (n² + n)/2 grows like n² as n increases.
For example, as n increases from 1,000 to 1,000,000
(n² + n) / 2 increases from 500500 to 500000500000
(n²) / 2 increases from 500000 to 500000000000
(n²) increases from 1000000 to 1000000000000
Similarly, as n increases from 1,000,000 to 1,000,000,000
(n² + n) / 2 increases from 500000500000 to 500000000500000000
(n²) / 2 increases from 500000000000 to 500000000000000000
(n²) increases from 1000000000000 to 1000000000000000000
They grow similarly, which is what Big O Notation is about.
If you plot (n²+n)/2 and n²/2 on Wolfram Alpha, they are so similar that they're difficult to distinguish by n=100. If you plot all three on Wolfram Alpha, you see two lines separated by a constant factor of 2.
3rd Person thought:
use of an equal sign, which is not used here to denote the equality of functions.
As you know, this notation expresses an asymptotic comparisons of functions, and writing f = O(g)means that f(n) grows at most as fast as g(n) as n goes to infinity.
This is pretty much like saying that 2 = 5 mod 3 does not imply that 2 = 5 and if you are keen on algebra, you can actually understand the big O notation as an equality modulo something.
What is Big 0 from Rob Bell:
As a programmer first and a mathematician second (or maybe third or fourth) I found the best way to understand Big O thoroughly was to produce some examples in code. So, below are some common orders of growth along with descriptions and examples where possible.
O(1)
O(1) describes an algorithm that will always execute in the same time (or space) regardless of the size of the input data set.bool IsFirstElementNull(IList<string> elements)
{
return elements[0] == null;
}
O(N)
O(N) describes an algorithm whose performance will grow linearly and in direct proportion to the size of the input data set. The example below also demonstrates how Big O favours the worst-case performance scenario; a matching string could be found during any iteration of thefor loop and the function would return early, but Big O notation will always assume the upper limit where the algorithm will perform the maximum number of iterations.bool ContainsValue(IList<string> elements, string value)
{
foreach (var element in elements)
{
if (element == value) return true;
}
return false;
}
O(N2)
O(N2) represents an algorithm whose performance is directly proportional to the square of the size of the input data set. This is common with algorithms that involve nested iterations over the data set. Deeper nested iterations will result in O(N3), O(N4) etc.bool ContainsDuplicates(IList<string> elements)
{
for (var outer = 0; outer < elements.Count; outer++)
{
for (var inner = 0; inner < elements.Count; inner++)
{
// Don't compare with self
if (outer == inner) continue;
if (elements[outer] == elements[inner]) return true;
}
}
return false;
}
O(2N)
O(2N) denotes an algorithm whose growth doubles with each additon to the input data set. The growth curve of an O(2N) function is exponential - starting off very shallow, then rising meteorically. An example of an O(2N) function is the recursive calculation of Fibonacci numbers:int Fibonacci(int number)
{
if (number <= 1) return number;
return Fibonacci(number - 2) + Fibonacci(number - 1);
}
Logarithms
Logarithms are slightly trickier to explain so I'll use a common example:Binary search is a technique used to search sorted data sets. It works by selecting the middle element of the data set, essentially the median, and compares it against a target value. If the values match it will return success. If the target value is higher than the value of the probe element it will take the upper half of the data set and perform the same operation against it. Likewise, if the target value is lower than the value of the probe element it will perform the operation against the lower half. It will continue to halve the data set with each iteration until the value has been found or until it can no longer split the data set.
This type of algorithm is described as O(log N). The iterative halving of data sets described in the binary search example produces a growth curve that peaks at the beginning and slowly flattens out as the size of the data sets increase e.g. an input data set containing 10 items takes one second to complete, a data set containing 100 items takes two seconds, and a data set containing 1000 items will take three seconds. Doubling the size of the input data set has little effect on its growth as after a single iteration of the algorithm the data set will be halved and therefore on a par with an input data set half the size. This makes algorithms like binary search extremely efficient when dealing with large data sets.

